Convergence Rates of Gaussian ODE Filters
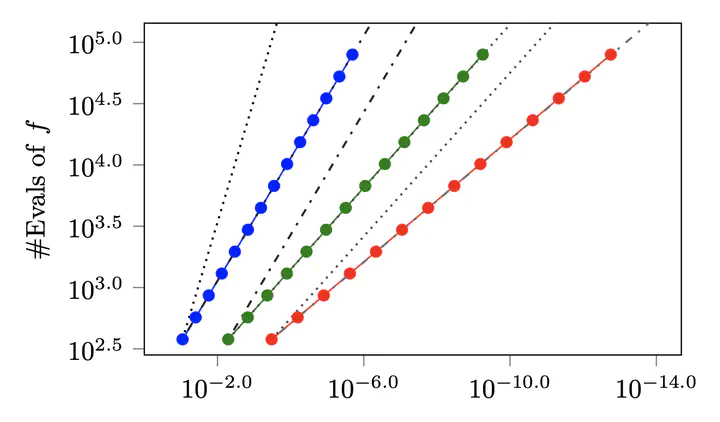 If q derivatives are modelled, ODE filters have $q$th-order global convergence rates.
If q derivatives are modelled, ODE filters have $q$th-order global convergence rates.
Abstract
A recently-introduced class of probabilistic (uncertainty-aware) solvers for ordinary differential equations (ODEs) applies Gaussian (Kalman) filtering to initial value problems. These methods model the true solution $x$ and its first $q$ derivatives a priori as a Gauss–Markov process $\boldsymbol{X}$, which is then iteratively conditioned on information about $\dot{x}$. This article establishes worst-case local convergence rates of order $q+1$ for a wide range of versions of this Gaussian ODE filter, as well as global convergence rates of order $q$ in the case of $q=1$ and an integrated Brownian motion prior, and analyses how inaccurate information on $\dot{x}$ coming from approximate evaluations of $f$ affects these rates. Moreover, we show that, in the globally convergent case, the posterior credible intervals are well calibrated in the sense that they globally contract at the same rate as the truncation error. We illustrate these theoretical results by numerical experiments which might indicate their generalizability to $q \in {2,3,\dots}$.