Uncertainty-Aware Numerical Solutions of ODEs by Bayesian Filtering
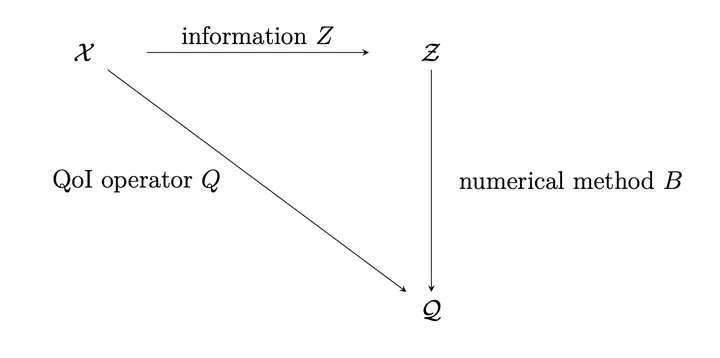 Conceptual diagram for probabilistic numerical methods
Conceptual diagram for probabilistic numerical methods
Abstract
We formulate probabilistic numerical approximations to solutions of ordinary differential equations (ODEs) as problems in Gaussian process (GP) regression with nonlinear measurement functions. This is achieved by defining the measurement sequence to consist of the observations of the difference between the derivative of the GP and the vector field evaluated at the GP—–which are all identically zero at the solution of the ODE. When the GP has a state-space representation, the problem can be reduced to a nonlinear Bayesian filtering problem and all widely used approximations to the Bayesian filtering and smoothing problems become applicable. Furthermore, all previous GP-based ODE solvers that are formulated in terms of generating synthetic measurements of the gradient field come out as specific approximations. Based on the nonlinear Bayesian filtering problem posed in this paper, we develop novel Gaussian solvers for which we establish favourable stability properties. Additionally, non-Gaussian approximations to the filtering problem are derived by the particle filter approach. The resulting solvers are compared with other probabilistic solvers in illustrative experiments.