Active Uncertainty Calibration in Bayesian ODE Solvers
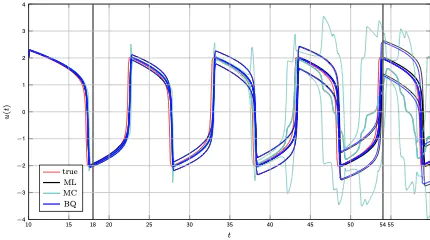 Active uncertainty calibration by Bayesian quadrature
Active uncertainty calibration by Bayesian quadrature
Abstract
There is resurging interest, in statistics and machine learning, in solvers for ordinary differential equations (ODEs) that return probability measures instead of point estimates. Recently, Conrad et al. introduced a sampling-based class of methods that are ‘well-calibrated’ in a specific sense. But the computational cost of these methods is significantly above that of classic methods. On the other hand, Schober et al. pointed out a precise connection between classic Runge–Kutta ODE solvers and Gaussian filters, which gives only a rough probabilistic calibration, but at negligible cost overhead. By formulating the solution of ODEs as approximate inference in linear Gaussian SDEs, we investigate a range of probabilistic ODE solvers, that bridge the trade-off between computational cost and probabilistic calibration, and identify the inaccurate gradient measurement as a crucial source of uncertainty. We propose the novel filtering-based method Bayesian Quadrature filtering (BQF) which uses Bayesian quadrature to actively learn the imprecision in the gradient measurement by collecting multiple gradient evaluations.